Welcome

Mahmoud S. M. Shaqfa

About

I obtained my Bachelor’s degree in Civil Engineering at the Islamic University of Gaza (IUG) in 2014. Later, I received my Master’s in Structural Engineering from the University of Pécs in 2017 (Hungary). In 2018, I moved to Switzerland to pursue my Ph.D. at École Polytechnique Fédérale de Lausanne (EPFL), conducting research at the Earthquake Engineering and Structural Dynamics (EESD) Laboratory under the supervision of Prof. Katrin Beyer from 2018 to 2022.

After that, I briefly worked as a postdoctoral fellow at EESD for 4 months. In 2023, after being awarded the prestigious PostDoc.Mobility grant from the Swiss National Science Foundation (SNSF), I moved to the USA to join the van Rees Laboratory (led by Prof. Wim van Rees at MIT).

Currently, I work with Prof. Josip Atalić as a scientist at the Croatian Centre for Earthquake Engineering at the University of Zagreb (UniZg).

Contact

• 📧 Email (personal): msshaqfa@hotmail.com
• 📧 Email (academic): mshaqfa@mit.edu

Research Theses and Proposals

1. M.Sc.: Design of reinforced concrete beams using metaheuristic algorithms (Prof. Zoltan Orban, PTE, 2018)

2. Ph.D.: Geometrical treatise on the modelling of 3D particulate inclusion-matrix microstructures with an application to historical stone masonry walls (Prof. Katrin Beyer, EPFL, 2022)

3. PostDoc: Harmonic decomposition of the 3D morphology of surfaces for simulating the growth of soft shells and plates (Prof. Wim M. van Rees, MIT, 2024)

Research Works and Interests

During my academic career, I developed an interest in a variety of topics, all of which converge around geometry, shapes, topology, and optimization problems—often with an engineering flavor. These areas demand in-depth knowledge of numerical methods such as Galerkin approaches, Discrete Exterior Calculus, and spectral methods.

Keywords: Solid Mechnanics, Fractal surfaces, Morphology, Computational geometry, Metaheuristics, Optimization, Fracture mechanics, Masonry structures, Rough contacts, CAD.

Science Gallery

Manifold harmonics (MH)

This ongoing work focuses on surface parametrization, with further results and details to be presented in due course.

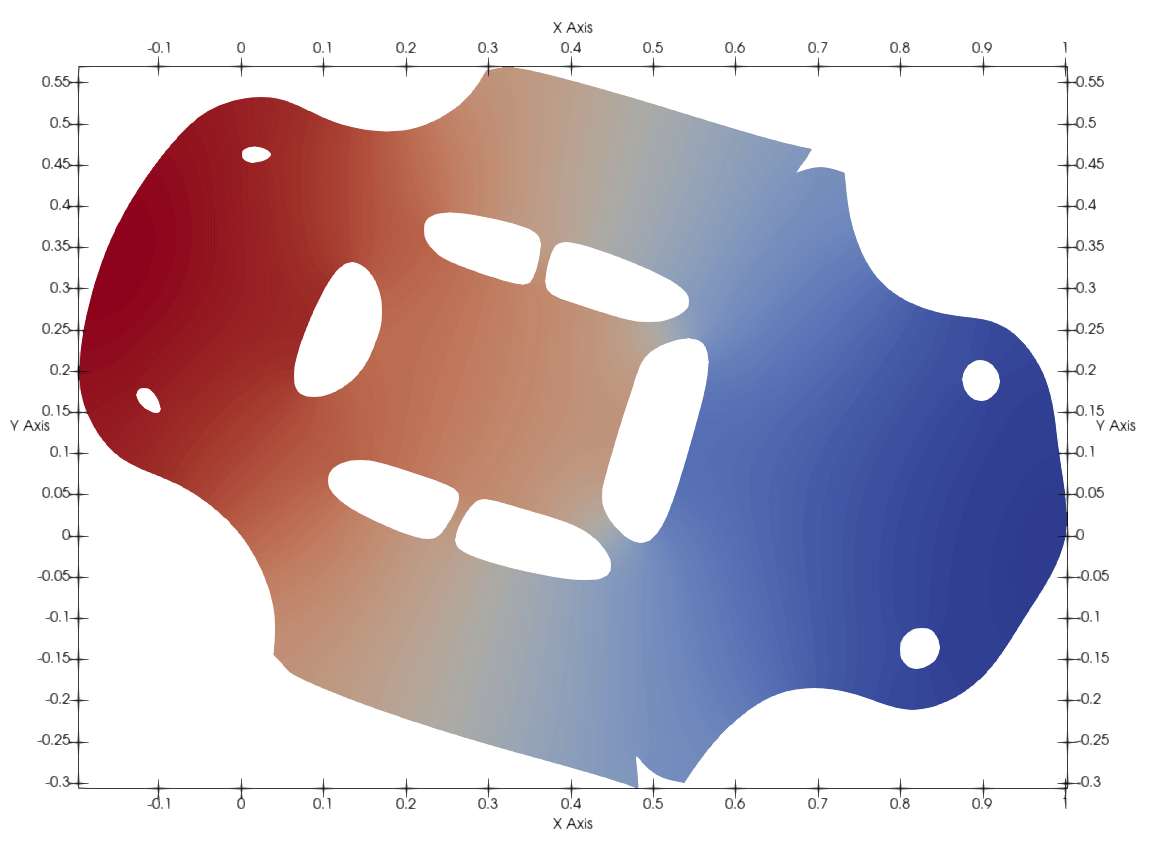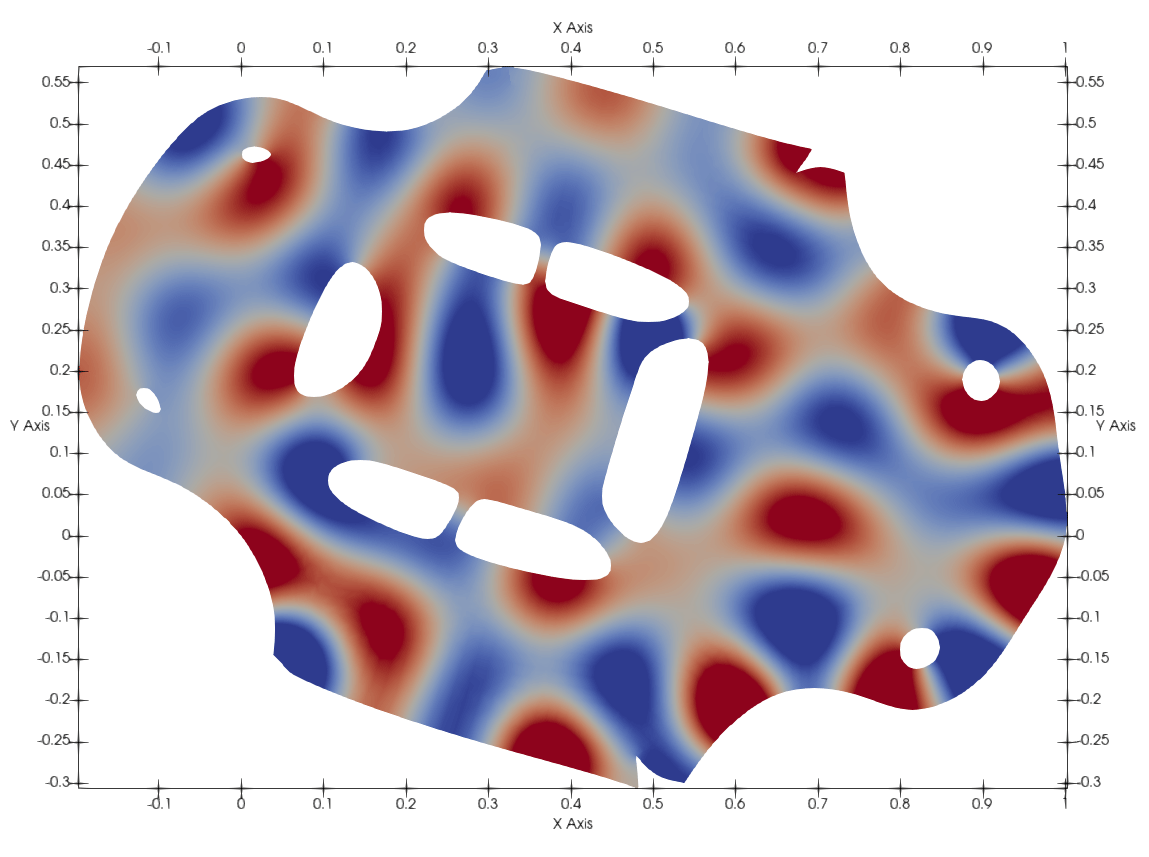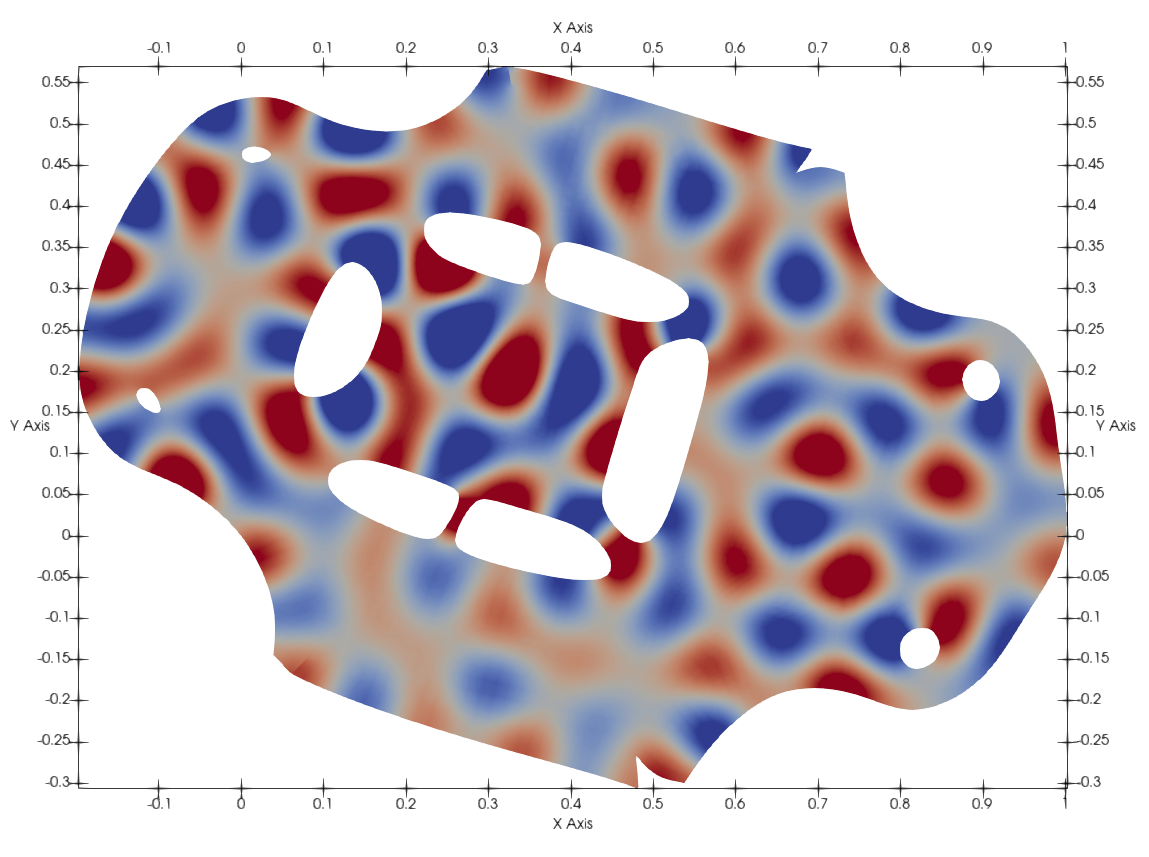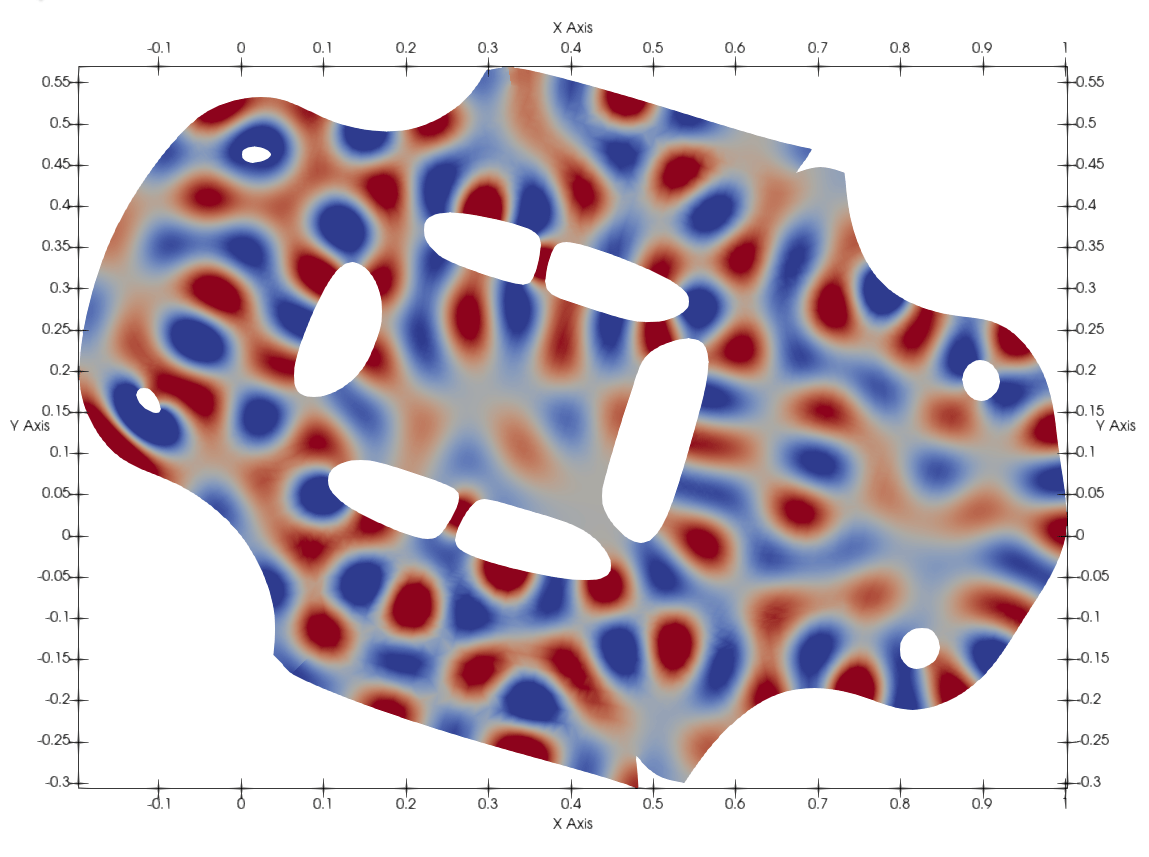
Harmonic basis (Eigen problem)

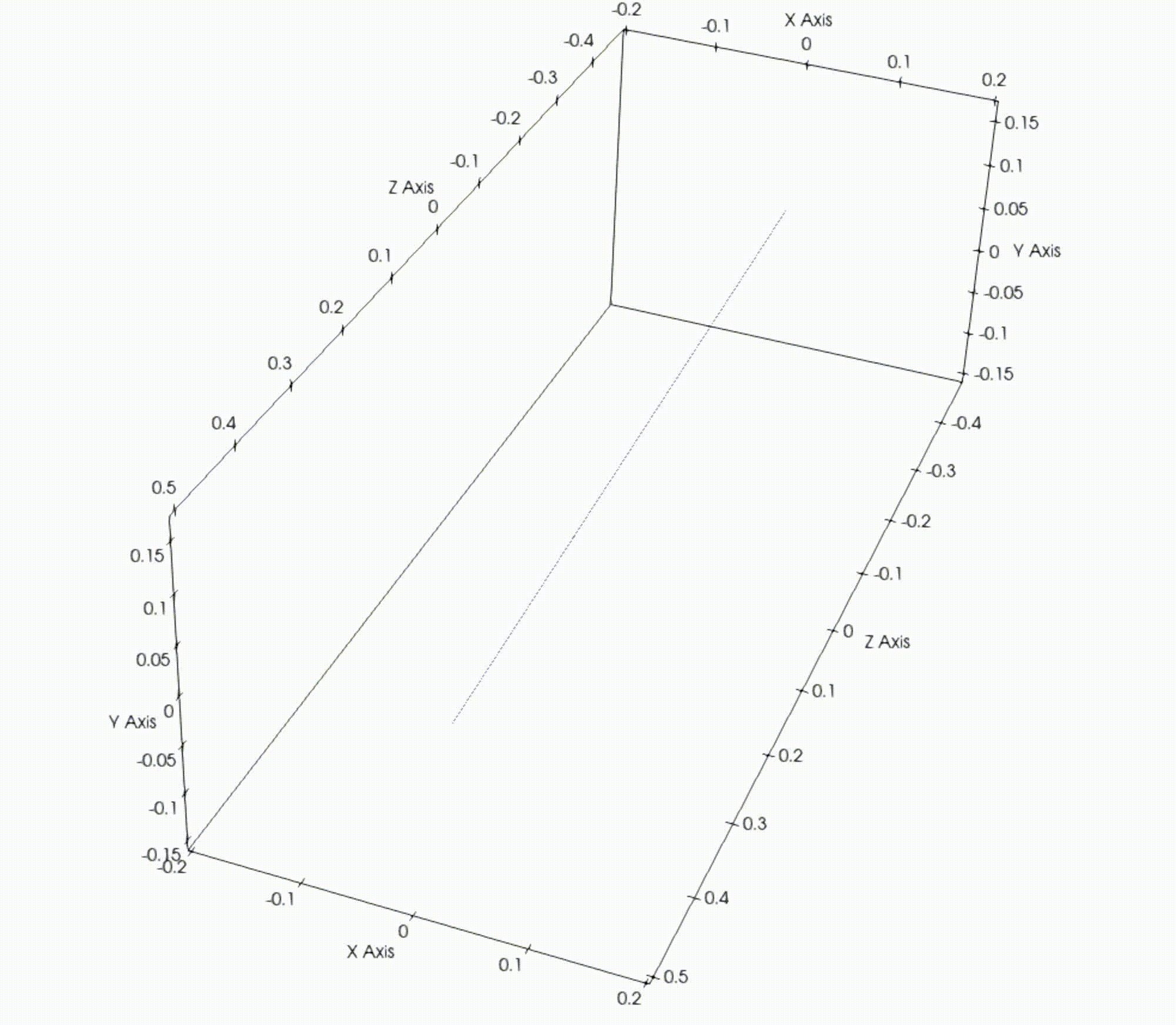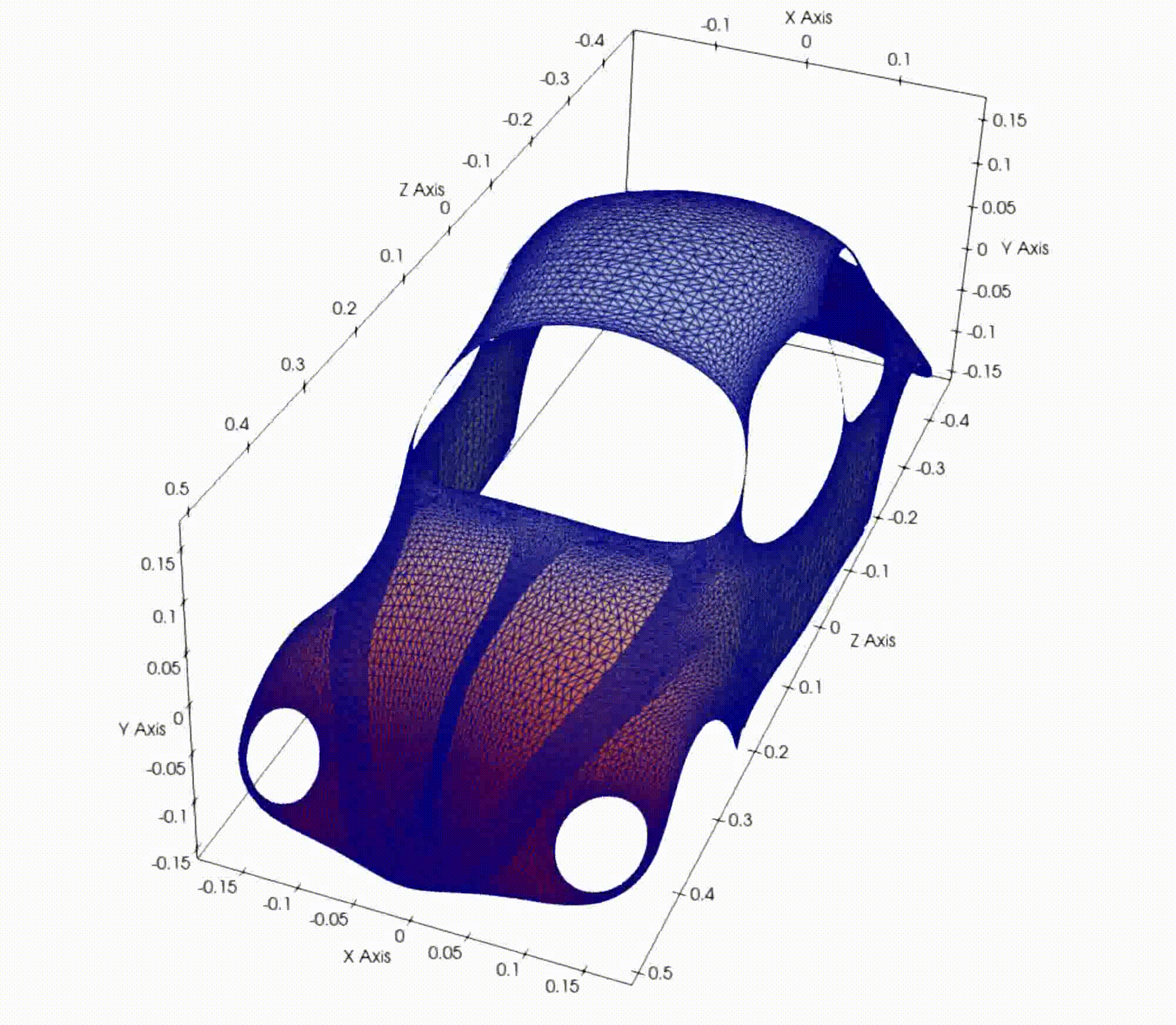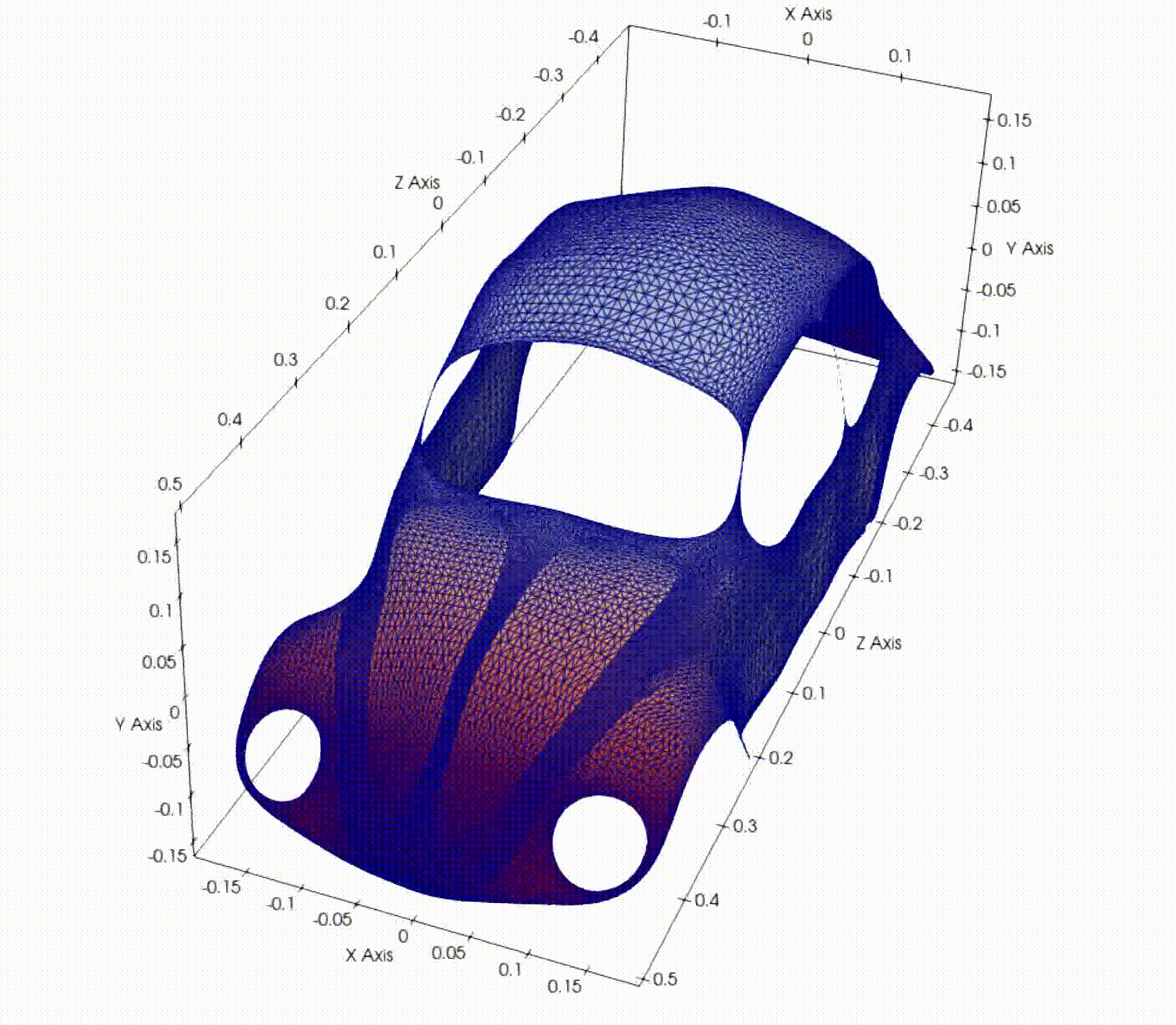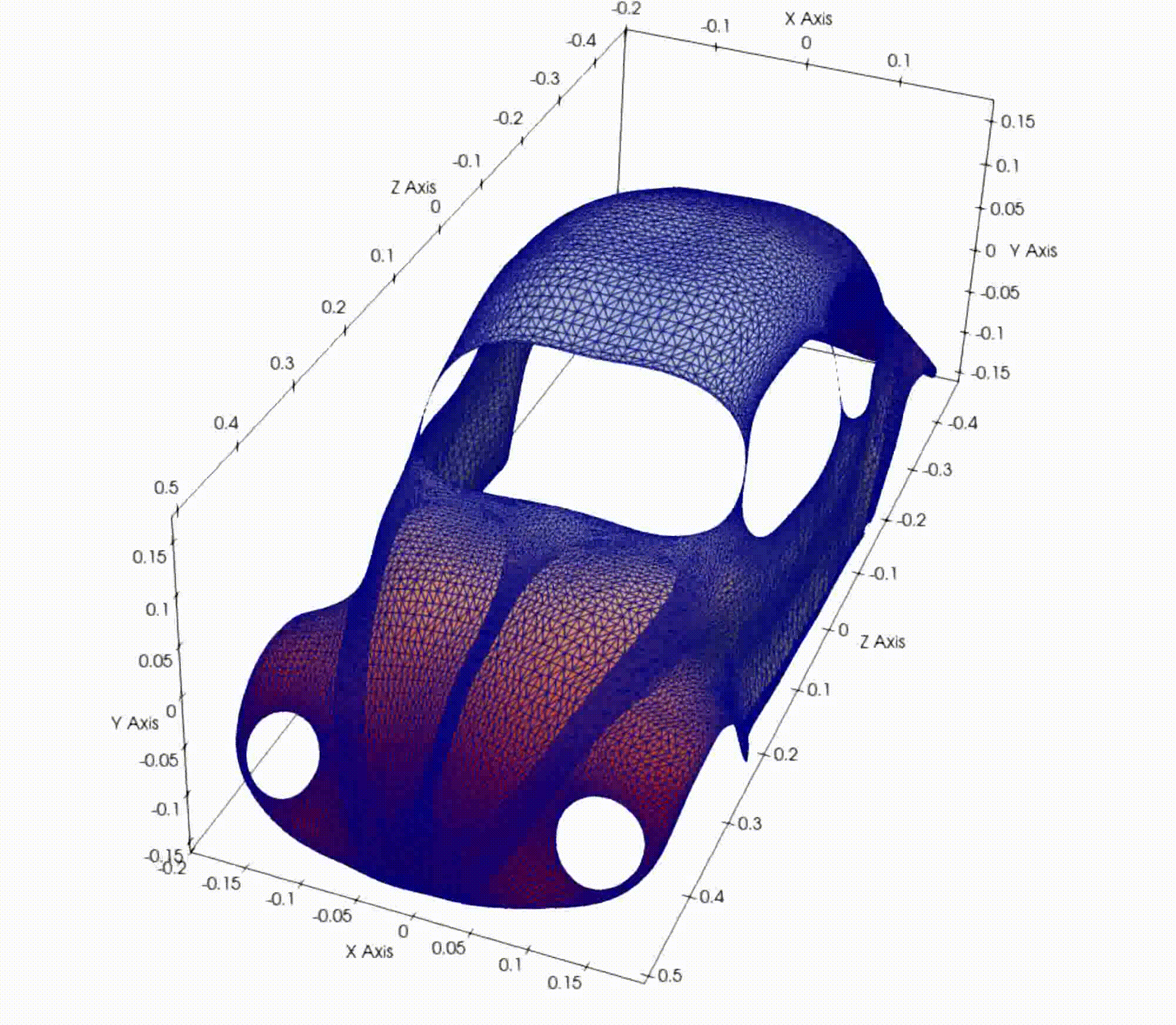
Harmonic reconstruction

Spheroidal harmonics (SOH)

This is from our new paper [1] that generalizes the traditional spherical harmonics approach (SH).

Surface reconstruction of Max Planck's head bust

Remeshing microstructures of 2D contours

Remeshing of closed contours to generate and parameterize 2D microstructures. In the Figure below, the first two rows show how the contours morph from low to high frequencies (k) and how the number of segment (s) affects the reconstruction; the contours were expanded with a maximum 2⁷ harmonics. The last row shows the corresponding FEM mesh for different frequencies and segments to control the mesh refinements.

Coming soon: Uniform remeshing of surfaces and contours via the harmonic decomposition approaches

The reconstructed meshes via the harmonic approaches are neither optimal nor uniform. To have a high-quality mesh, we proposed a morphology-preserving meshing approach. This approach uses the analogy of the heat problem to diffuse the surface points equidistantly on the reconstructed surfaces/contours. This work is still under review, and a preprint will be soon available. The following are some of the obtained results:

Uniform sampling of the dolphin's 2D contour via the Elliptic Fourier approach

The following is a 3D example for remeshing the above reconstruction of Max Planck’s head bust:

Uniform sampling of 2-manifold (3D surface) via the SOH approach [1]

References

[1] Mahmoud Shaqfa and Wim M. van Rees. Spheroidal harmonics for generalizing the morphological decomposition of closed parametric surfaces. Construction and Building Materials, Vol. 454, 2024, Article 138967. https://doi.org/10.1016/j.conbuildmat.2024.138967